Liczby zmiennoprzecinkowe

Artykuł ten wymaga znajomości notacji binarnej. Jeśli jeszcze jej nie znasz koniecznie zapoznaj się z artykułem opisującym system binarny.

Artykuł ten ma Cię jedynie wprowadzić w tematykę związaną ze standardem IEEE754. Nie poruszam w nim kwestii związanych z arytmetyką, zaokrąglaniem czy wartościami specjalnymi.

Celem tego artykułu jest wytłumaczenie dlaczego operacje na liczbach zmiennoprzecinkowych nie są dokładne. Jeśli szukasz bardziej szczegółowych informacji odsyłam do punktu “Dodatkowe materiały do nauki”.

Niezbędne podstawy

Odrobina matematyki

Żeby móc mówić o liczbach zmiennoprzecinkowych należy zrozumieć czym są liczby wymierne. Liczba wymierna to liczba, którą można przedstawić w postaci ułamka zwykłego. Dla przypomnienia to ten ułamek z kreską poziomą, który ma licznik i mianownik. Przykładem ułamka zwykłego jest ½.

Ułamki mają jeszcze postać dziesiętną. Przykładem ułamka dziesiętnego jest 0,5.

Niektóre ułamki zwykłe nie mają skończonej reprezentacji jako ułamek dziesiętny. Na przykład ułamek ⅓ zapisany dziesiętnie ma postać 0,(3). Taka notacja oznacza, że ułamek dziesiętny ma rozwinięcie okresowe. Zawartość nawiasu powtarzana jest w nieskończoność 0,33333.... Okres ułamka może mieć kilka cyfr, na przykład 0,38(12). Taki okres rozwija się do ułamka 0,3812121212....

Liczby wymierne zapisywane binarnie

Liczby wymierne można zapisać także binarnie. Algorytm na zamianę liczb całkowitych z postaci dziesiętnej na postać binarną opisałem w artykule na temat systemu binarnego. Do zamiany zostaje część po przecinku. Weźmy na przykład liczbę 0,25. Aby zapisać ją binarnie należy postępować zgodnie z algorytmem:

1. Zapisz 0,,
2. Pomnóż ułamek przez 2, jeśli wynik jest większy bądź równy 1 należy dopisać 1 w reprezentacji binarnej. W przeciwnym wypadku należy dopisać 0.
3. Jeśli wynik jest równy 1 jest to koniec algorytmu. Jeśli wynik jest mniejszy od 1 należy przejść do punktu drugiego. Jeśli wynik jest większy od 1 należy odjąć od niego 1 i przejść do punktu drugiego.

Mam nadzieję, że przykład pozwoli Ci lepiej zrozumieć zasadę działania algorytmu. Zacznijmy od liczby 0,75.

1. Postać binarna 0,,
2. 0,75 * 2 = 1,5. Wynik jest większy od 1 więc dopisuję 1. Postać binarna 0,1. Wynik jest większy od 1 więc odejmuję jedynkę: 1,5 - 1 = 0,5,
3. 0,5 * 2 = 1. Wynik jest równy 1 więc dopisuję 1. Postać binarna 0,11. Wynik jest równy 1 więc to koniec algorytmu,
4. 0,75 zapisane jako ułamek binarny to 0,11.

Inny przykład, tym razem ułamek dziesiętny to 0,125:

1. Postać binarna 0,,
2. 0,125 * 2 = 0,25. 0,25 < 1 więc dopisuję 0. Postać binarna to 0,0,
3. 0,25 * 2 = 0,5. 0,5 < 1 więc dopisuję 0. Postać binarna to 0,00,
4. 0,5 * 2 = 1. 1 == 1 więc dopisuję 1. Postać binarna to 0,001, koniec algorytmu,
5. 0,125 zapisane jako ułamek binarny to 0,001.

Nie wszystkie ułamki, które mają skończone rozwinięcie dziesiętne są skończone w postaci binarnej. Spójrz jak wygląda to w przypadku ułamka 0,1:

1. Postać binarna 0,,
2. 0,1 * 2 = 0,2. 0,2 < 1 więc dopisuję 0. Postać binarna to 0,0,
3. 0,2 * 2 = 0,4. 0,4 < 1 więc dopisuję 0. Postać binarna to 0,00,
4. 0,4 * 2 = 0,8. 0,8 < 1 więc dopisuję 0. Postać binarna to 0,000,
5. 0,8 * 2 = 1,6. 1,6 > 1 więc dopisuję 1 i odejmuję 1 od wyniku. Postać binarna to 0,0001,
6. 0,6 * 2 = 1,2. 1,2 > 1 więc dopisuję 1 i odejmuję 1 od wyniku. Postać binarna to 0,00011,
7. Ułamek 0,2 występował już w kroku 3. Jeśli liczba się powtarza mamy do czynienia z ułamkiem, który ma nieskończone rozwinięcie binarne. Postać binarna to 0,0(0011).

Aby zapisać liczbę wymierną, która ma zarówno część całkowitą i ułamkową należy połączyć zapis części całkowitej i ułamkowej. Na przykład liczba 20,1 zapisana binarnie to 10100,0(0011). Jest to tak zwana stałoprzecinkowa reprezentacja liczby wymiernej.

Notacja naukowa a liczby wymierne

W matematyce poza standardowym zapisem liczb, który już znasz 10, 123,15 czy 0,00000827194 istnieje tak zwana notacja naukowa. Jest ona pomocna przy zapisywaniu bardzo dużych/małych liczb w stosunkowo zwięzłej formie. Na przykład liczbę 0,00000827194 można zapisać jako (8,27194 * 10^{-6}). Inna postać tej liczby to 8,27194e-6.

W języku Java możesz zobaczyć jak dana liczba wygląda w postaci naukowej:

System.out.println(String.format("%e", 123.456));

Po uruchomieniu powyższego kodu na konsoli pokaże się:

1.234560e+02

Pobierz opracowania zadań z rozmów kwalifikacyjnych

Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.

Czym jest standard IEEE754

Standard IEEE754 jest standardem opisującym arytmetykę zmiennoprzecinkową. W dużym uproszczeniu można powiedzieć, że opisuje on sposób zapisywania liczby wymiernej w pamięci komputera. Standard ten może być implementowany już na poziomie sprzętowym. Oznacza to tyle, że procesor może mieć specjalną jednostkę odpowiedzialną za obliczenia zmiennoprzecinkowe.

Standard ten opisuje kilka formatów zapisu liczb. Jednym z nich jest zapis pojedynczej precyzji gdzie do zapisania liczby używa się 32 bitów. Występuje też wersja z podwójną precyzją, gdzie używa się 64 bitów do zapisania liczby.

W języku Java liczby typu float są liczbami zmiennoprzecinkowymi formacie pojedynczej precyzji. Liczby typu double to liczby zmiennoprzecinkowe zapisane na 64 bitach w formacie podwójnej precyzji.

W dalszej części artykułu skupię się wyłącznie na liczbach zmiennoprzecinkowych zapisanych w formacie pojedynczej precyzji.

Liczba zmiennoprzecinkowa

Liczba zmiennoprzecinkowa to liczba wymierna zapisana w formacie IEEE754. Nazwa zmiennoprzecinkowa wynika z tego, że miejsce przecinka w liczbie zmienia swoje położenie. Spójrz na przykład poniżej:

1234,567
1,234567e+3

Obie te liczby są równe, jednak przecinek w drugiej z nich znajduje się w innym miejscu. Druga liczba zapisana jest w notacji naukowej.

Części składowe liczby zmiennoprzecinkowej

Każdą liczbę zmiennoprzecinkową zapisujemy w pamięci przy pomocy trzech składowych:

• znaku,
• wykładnika,
• mantysy.

Liczba zmiennoprzecinkowa pojedynczej precyzji © Wikipedia

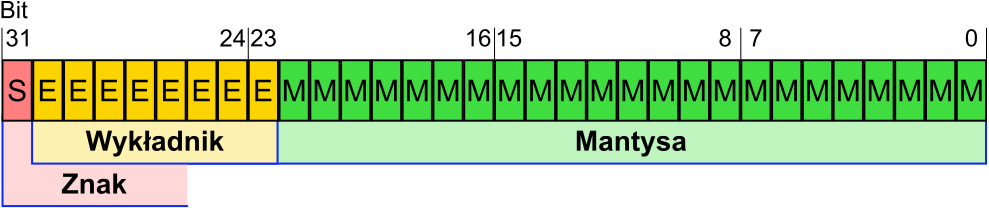
Wartość liczby zmiennoprzecinkowej zależy od wartości poszczególnych pól. Można ją zapisać przy pomocy wzoru:

\[-1^{znak} * 2^{wykładnik} * mantysa\]

Wzór ten przypomina notację naukową.

Znak

Liczby mogą być dodanie, ujemne lub 0. Znak służy do określenia czy dana liczba jest dodania czy ujemna. Jeśli liczba jest dodatnia bit znaku zawiera 0.

Wykładnik

Wykładnik to liczba zapisana na ośmiu bitach. Używa się tu tak zwanego kodowania z nadmiarem. W tym przypadku nadmiar wynosi -127. Oznacza to, że od zakodowanej liczby należy odjąć liczbę 127 aby uzyskać zakodowaną wartość. Standardowo na ośmiu bitach możemy zapisać liczbę (2^8 -1 == 255). Używając kodowania z nadmiarem -127 na ośmiu bitach możemy zakodować liczby z zakresu [-127, 128].

Innymi słowy wykładnik w liczbie zmiennoprzecinkowej może być z zakresu -127 do 128¹.

Mantysa

Mantysa zapisana jest na 23 bitach. Zawiera ona właściwą liczbę, która zostanie pomnożona przez wykładnik zgodnie ze wzorem podanym wyżej.

Mantysa w większości przypadków ma postać znormalizowaną. Najłatwiej będzie mi to wytłumaczyć na przykładzie. Załóżmy, że mamy liczbę zapisaną binarnie 1011,1101. Znormalizowana postać tej liczby to (1,0111101 * 2^3). Jak widzisz przecinek przesunięty jest do pierwszej jedynki.

Inny przykład to 0,0001010110001, która po normalizacji wygląda następująco (1,010110001 * 2^{-4}).

W znormalizowanej mantysie pierwszą cyfrą jest zawsze 1. W związku z tym jest pomijana. Zatem mając liczbę 1,010110001 mantysa będzie miała wartość (spacje dla czytelności):

0101 1000 1000 0000 0000 000

Część ułamkowa 010110001 została uzupełniona zerami aby zapełnić wszystkie 23 bity przeznaczone na mantysę.

Zapis liczby zmiennoprzecinkowej

Teraz masz już wszystkie informacje potrzebne do zapisania liczby zmiennoprzecinkowej. Zacznijmy od liczby 270,125. Liczba ta zapisana binarnie to 100001110,001. Po znormalizowaniu otrzymujemy

\[1,00001110001 * 2^{8}\]

W naszym przypadku po przecinku mamy 11 cyfr. Mantysę zapisujemy na 23. Brakujące miejsca uzupełniamy zerami. Więc mantysa będzie miała następującą postać (spacje dla czytelności):

0000 1110 0010 0000 0000 000

Nasz wykładnik to 8. Wynika on z przesunięcia w związku z normalizacją mantysy. Pamiętając o sposobie kodowania wykładnika dodaję do niego 127. Kodując 135 binarnie uzyskuję (spacja dla czytelności):

1000 0111

Nasza liczba jest dodania, więc bit znaku ma wartość 0.

Zbierając te informacje razem mogę zapisać liczbę 270,125 w standardzie IEEE754. Zapis ten wygląda następująco (spacje dla czytelności):

0  1000 0111  0000 1110 0010 0000 0000 000

Dlaczego 0,1 + 0,2 != 0,3

Standard IEEE754 bardzo ułatwił pracę z liczbami wymiernymi. Niestety ma on swoje wady. Jedną z nich jest to, że w pewnych przypadkach zapis liczby w tym formacie prowadzi do utracenia informacji. Dzieje się tak na przykład w przypadku gdy ułamek zapisany binarnie ma rozwinięcie okresowe. Przykładem takich ułamków są 0,1 czy 0,2.

Proszę spójrz na przykłady poniżej. Używam tu kodu Javy, jednak właściwość ta jest prawdziwa także w innych językach programowania:

System.out.println(String.format("%.17f" , 0.1F));
System.out.println(String.format("%.17f" , 0.2F));
System.out.println(String.format("%.17f" , 0.3F));

0.10000000149011612
0.20000000298023224
0.30000001192092896

Jeśli chcesz wiedzieć czym jest magiczne "%.17f" zachęcam Cię do przeczytania artykułu na temat formatowania łańcuchów znaków w języku Java.

Jak widzisz wprowadzone 0,1 trochę różni się od właściwej wartości zapisanej w pamięci komputera. Chociaż 0,1 + 0,2 == 0,3 to w pamięci komputera wygląda to trochę inaczej:

0.10000000149011612 + 0.20000000298023224 != 0.30000001192092896

Rady praktyczne

W związku z opisanymi problemami typy double czy float nie zawsze są dobrym wyborem. Na przykład pisząc aplikację do banku, która oblicza ratę kredytu na pewno nie powinieneś używać tych typów. Z pomocą przychodzi klasa BigDecimal. Jeśli zależy Ci na dokładnych obliczeniach w większości przypadków będzie to dobry wybór:

System.out.println(new BigDecimal("0.1"));

Wyświetli oczekiwane

0.1

Proszę zwróć uwagę na sposób tworzenia instancji BigDecimal. Używam tutaj konstruktora, który przyjmuje liczbę jako łańcuch znaków. Użycie klasy BigDecimal utworzonej na podstawie instancji float powtórzy błąd:

System.out.println(new BigDecimal(0.1F));

0.100000001490116119384765625

Innym sposobem na pracę z liczbami wymiernymi jest użycie typów całkowitoliczbowych. Jest to możliwe w przypadku gdy wiesz ile miejsc po przecinku jest dla Ciebie ważne. Na przykład operacje pieniężne w większości przypadków potrzebują dwóch miejsc po przecinku. Zatem kwotę 125 złotych 68 groszy możemy zapisać jako 12568 i przechowywać w polu o typu int czy long. Przy pomocy dzielenia możemy uzyskać część całkowitoliczbową i część ułamkową:

int money = 12568;

System.out.println("zlotych: " + money / 100);
System.out.println("groszy: " + money % 100);

Dodatkowe materiały do nauki

Jeśli chcesz spojrzeć na temat liczb zmiennoprzecinkowych z innej perspektywy możesz rzucić okiem na poniższe materiały:

• artykuł na Wikipedii na temat liczb zmiennoprzecinkowych,
• artykuł na Wikipedii na temat standardu IEEE754,
• artykuł opisujący standard IEEE754,
• treść najnowszej wersji standardu IEEE754 (wymaga wykupienia dostępu).

Zadania do wykonania

Do wykonania zadań mogą Ci się przydać następujące funkcje:

• Integer.toBinaryString,
• Long.toBinaryString,
• Float.floatToRawIntBits.
• Double.doubleToRawLongBits,

Zadania do wykonania:

1. Napisz program, który pobierze od użytkownika liczbę wymierną. Następnie wypisze tę liczbę w postaci binarnej pokazując osobno znak, wykładnik i mantysę.
2. Uzupełnij program z punktu 1. w ten sposób, aby pokazywał błąd wynikający z zapisu liczb. Na przykład jeśli użytkownik wprowadzi liczbę 0,1 wówczas program powinien wyświetlić binarną reprezentację i błąd powstały w wyniku zapisu liczby w tym formacie,
3. Spróbuj rozszerzyć program w ten sposób aby wspierał liczby zmiennoprzecinkowe zapisane w formacie podwójnej precyzji (1 bit znaku, 11 bitów wykładnika i 52 bity mantysy).

Zachęcam Cię do samodzielnego rozwiązania zadań, wtedy nauczysz się najwięcej. Jeśli jednak będziesz potrzebował pomocy możesz rzucić okiem na przykładowe rozwiązanie na githubie.

Podsumowanie

Po przeczytaniu artykułu wiesz już czym są liczby zmiennoprzecinkowe. Znasz podstawy standardu IEEE754. Wiesz dlaczego niektóre operacje na liczbach zmiennoprzecinkowych nie są dokładne. Wiesz także jak wykonywać dokładne operacje na liczbach wymiernych. Innymi słowy kawał wiedzy! :).

Mam nadzieję, że artykuł przypadł Ci do gustu. Proszę podziel się nim ze swoimi znajomymi, którzy mogą być nim zainteresowani. Jeśli nie chcesz pominąć nowych artykułów polub Samouczka na Facebooku i dopisz się do samouczkowego newslettera.

Do następnego razu!

1. Jak już wspomniałem wcześniej dotyczy to liczb zapisanych w formacie pojedynczej precyzji. ↩

Pobierz opracowania zadań z rozmów kwalifikacyjnych

Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.