Struktury danych
Lista wiązana to struktura danych. Struktury danych opisują sposób przechowywania danych w pamięci komputera. Przykładową strukturą danych jest tablica. Każda struktura danych ma charakterystyczne dla siebie właściwości. Na przykład dodanie elementu na początek tablicy ma złożoność obliczeniową Ο(n). Ta sama operacja dla listy wiązanej ma złożoność Ο(1)1.
Te właściwości sprawiają, że użycie konkretnej struktury może uprościć rozwiązanie niektórych problemów. Możemy powiedzieć, że czasami lepiej jest użyć tablicy a w innym przypadku lista wiązana jest lepszym rozwiązaniem. Wszystko zależy od problemu, który próbujemy rozwiązać. Strukturę danych dopasowuje się do problemu.
Klasyczną pozycją jeśli chodzi o powiązanie algorytmów i struktur danych jest książka autorstwa Niklausa Wirtha Algorytmy + struktury danych = programy.
Struktury danych w językach programowania
Struktura danych jest niezależna od języka programowania. Można ją zaimplementować w różnych językach. Na przykład tablica jest uniwersalną strukturą, która istnieje w każdym znanym mi języku programowania.
Podobnie sytuacja wygląda z listą wiązaną. Przeważnie w standardowej bibliotece danego języka znajdzie się już gotowa implementacja tej struktury danych. W języku Java implementacją dwukierunkowej listy wiązanej jest klasa LinkedList. O tym czym jest dwukierunkowa lista wiązana przeczytasz w jednym z akapitów poniżej.
Skoro zatem mamy gotowe implementacje to po co pisać kolejną? Jedynym powodem jest nauka i zrozumienie zasady działania danej struktury danych. Jeśli dany język dostarcza implementacji danej struktury najlepszym sposobem będzie jej użycie. Nie wymyślaj koła na nowo :).
Struktury danych dostępne w standardowej bibliotece będą na pewno lepiej zaimplementowane niż własna wersja. Dodatkowo będą przetestowane przez dużo większą liczbę programistów.
Jak działa lista wiązana
Lista wiązana to struktura, która składa się z węzłów. Każdy z węzłów zawiera element, który przechowuje. Dodatkowo posiada także odnośniki do innych elementów. W ten sposób powstaje łańcuch powiązanych ze sobą węzłów. To ile odnośników przechowuje węzeł określa czy lista jest jedno, czy dwukierunkowa.
W dalszej części artykułu te odnośniki do sąsiednich elementów będę nazywał wskaźnikami.
Lista jednokierunkowa posiada wyłącznie wskaźnik do jednego elementu. Lista dwukierunkowa posiada dwa wskaźniki, do obu sąsiadujących elementów. Obrazki poniżej prezentują przykładowe listy z trzema elementami. Prostokąty to węzły, strzałki pokazują powiązania pomiędzy węzłami.
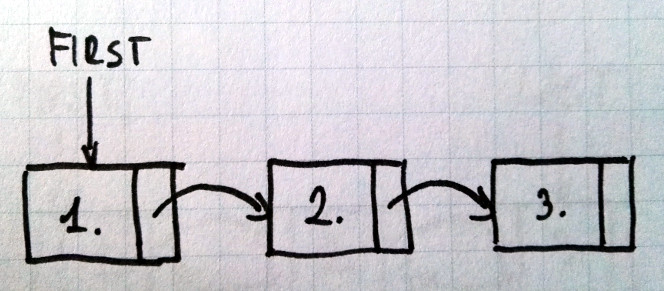
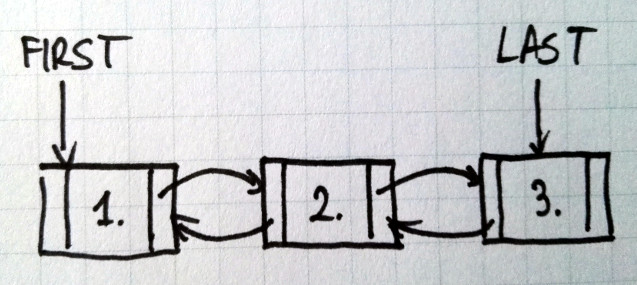
Lista wiązana jest strukturą, w której kolejność elementów ma znaczenie. Każdy z elementów ma swój numer, indeks, który zwyczajowo zaczyna się liczyć od 0.
Jeśli lista jest pusta wskaźnik na pierwszy/ostatni węzeł jest pusty (w przypadku Javy ma wartość null). Wskaźniki na następny/poprzedni węzeł w ostatnim/pierwszym węźle w liście są puste.
Lista jednokierunkowa
Jak już wiesz lista to powiązane ze sobą węzły. Przykładowa implementacja takiego węzła może wyglądać następująco:
private static class Node<E> {
private E element;
private Node<E> next;
Node(E element) {
this.element = element;
}
}
Klasa ta posiada element, atrybut ten przechowuje wartość z danego węzła. Każdy węzeł zawiera również wskaźnik do kolejnego węzła w liście. Kolejny węzeł przechowywany jest w atrybucie next.
Listę jednokierunkową w tym przypadku można przedstawić jako klasę, która zawiera informację o początku listy. W przykładzie poniżej pierwszy element z listy przechowywany jest w atrybucie first.
public class SingleLinkedList<E> {
private Node<E> first;
private static class Node<E> {
private E element;
private Node<E> next;
Node(E element) {
this.element = element;
}
}
}
Sprawdzanie czy lista jest pusta
Mając taką klasę w prosty sposób możemy sprawdzić czy lista zawiera jakiekolwiek elementy. Wystarczy sprawdzić czy pierwszy element istnieje:
public boolean isEmpty() {
return first == null;
}
Złożoność obliczeniowa tej operacji to Ο(1).
Sprawdzanie rozmiaru listy
Kolejną podstawową operacją jest sprawdzanie rozmiaru listy. Poniżej pokazuję naiwną implementację tej operacji:
public int size() {
int size = 0;
Node<E> currentNode = first;
while (currentNode != null) {
size++;
currentNode = currentNode.next;
}
return size;
}
Przechodząc po wszystkich elementach listy otrzymuję złożoność Ο(n)2.
Pobierz opracowania zadań z rozmów kwalifikacyjnych
Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.
Pobieranie elementu z listy
Wspomniałem wyżej, że lista wiązana jest strukturą, w której kolejność elementów jest istotna. Każdy z elementów ma swój indeks, podobnie jak w tablicy. Przydałaby się w takim razie metoda, która pozwoli pobrać element znajdujący się pod danym indeksem:
public E get(int index) {
if (isEmpty() || index < 0) {
throw new IndexOutOfBoundsException("Index " + index);
}
Node<E> currentNode = first;
int currentIndex = index;
while (currentIndex > 0) {
if (currentNode == null) {
throw new IndexOutOfBoundsException("Index " + index);
}
currentNode = currentNode.next;
currentIndex--;
}
return currentNode.element;
}
Pierwszy warunek sprawdza czy index ma szanse być poprawny. Następnie przechodząc przez kolejne elementy listy, zaczynając od początku dochodzę do elementu znajdującego się pod żądanym indeksem.
W związku z tym, że pętla while zależna jest od liczby elementów znajdujących się w liście złożoność tej operacji to Ο(n).
Dodawanie elementu do listy
Dodawanie nowego elementu do listy wiązanej zależy od tego gdzie chcemy taki element dodać. Rysunek poniżej pokazuje przykład dodawania elementu pomiędzy istniejącymi węzłami:
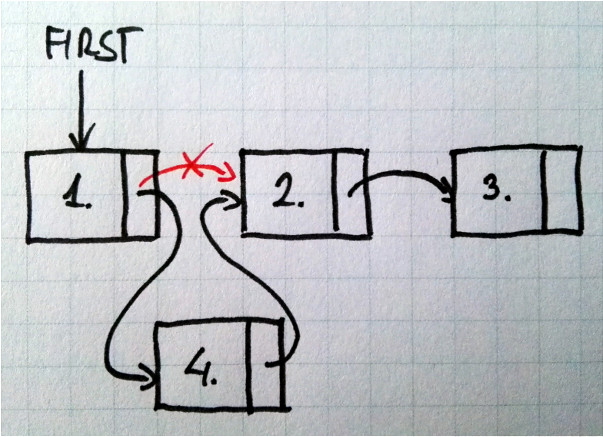
W takim przypadku należy w odpowiedni sposób przepiąć wskaźnik na kolejny element. Więc aby dodać element pod indeksem N potrzebuję dostęp do elementu pod indeksem N - 1. Metoda pomocnicza pozwala w łatwy sposób dostać się do obu węzłów:
private static class NodePair<E> {
private final Node<E> previous;
private final Node<E> current;
private NodePair(Node<E> previous, Node<E> current) {
this.previous = previous;
this.current = current;
}
}
private NodePair<E> getNodeWithPrevious(int index) {
if (isEmpty() || index < 0) {
throw new IndexOutOfBoundsException("Index " + index);
}
Node<E> previousNode = null;
Node<E> currentNode = first;
int currentIndex = index;
while (currentIndex > 0) {
if (currentNode == null) {
throw new IndexOutOfBoundsException("Index " + index);
}
previousNode = currentNode;
currentNode = currentNode.next;
currentIndex--;
}
return new NodePair<>(previousNode, currentNode);
}
Mając już metodę pomocniczą mogę zaimplementować dodawanie elementów do listy. Proszę spójrz na przykładową implementację poniżej:
public boolean add(int index, E element) {
if (first == null && index == 0) {
first = new Node<>(element);
return true;
}
NodePair<E> pair = getNodeWithPrevious(index);
Node<E> previousNode = pair.previous;
Node<E> nodeAtIndex = pair.current;
// adding at the beginning of the list
if (previousNode == null) {
first = new Node<>(element);
first.next = nodeAtIndex;
return true;
}
Node<E> newNode = new Node<>(element);
newNode.next = nodeAtIndex;
previousNode.next = newNode;
return true;
}
Pierwszy blok if obsługuje dodanie elementu do pustej listy. W tym przypadku po prostu tworzę nową instancję klasy Node i ustawiam ją jako atrybut first. Kolejny blok if obsługuje dodanie elementu na początku listy. W tym przypadku atrybut first musi być zmieniony. Resztę przypadków obsługują ostatnie linijki metody.
W przypadku tej implementacji dodanie elementu na początku listy ma złożoność Ο(1). Dodanie nowego elementu w innym miejscu to operacja o złożoności Ο(n).
Usuwanie elementu z listy
W przypadku usuwania elementu z listy również trzeba manipulować wskaźnikiem na kolejny element. Operację usuwanie pokazałem na rysunku poniżej:
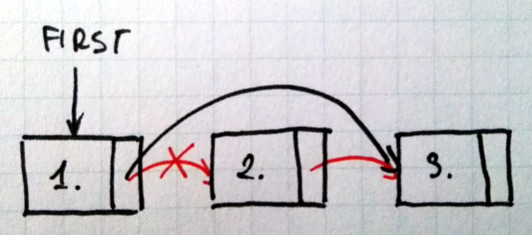
Także i tutaj pomocna jest metoda getNodeWithPrevious.
public E remove(int index) {
NodePair<E> pair = getNodeWithPrevious(index);
Node<E> previousNode = pair.previous;
Node<E> nodeToRemove = pair.current;
E removedElement = nodeToRemove.element;
// removing first node
if (previousNode == null) {
first = nodeToRemove.next;
return removedElement;
}
previousNode.next = nodeToRemove.next;
return removedElement;
}
Blok if obsługuje usunięcie pierwszego elementu z listy. W tym przypadku należy zmienić wartość atrybutu first.
W przypadku tej implementacji usunięcie elementu z początku listy ma złożoność Ο(1). Usunięcie elementu z innego miejsca to operacja o złożoności Ο(n).
Dwukierunkowa lista wiązana
Dwukierunkowa lista wiązana od listy jednokierunkowej różni się tym, że każdy z węzłów zawiera wskaźnik na poprzedni i następny element. Sama lista zawiera też atrybuty wskazujące pierwszy i ostatni węzeł w liście:
public class DoubleLinkedList<E> {
private Node<E> first;
private Node<E> last;
private static class Node<E> {
private E element;
private Node<E> next;
private Node<E> previous;
Node(E element) {
this.element = element;
}
}
}
Sprawdzanie czy lista jest pusta
Podobnie jak w przypadku listy jednokierunkowej, sprawdzenie czy lista ma pierwszy węzeł wystarczy:
public boolean isEmpty() {
return first == null;
}
Sprawdzanie rozmiaru listy
public int size() {
int size = 0;
Node<E> currentNode = first;
while (currentNode != null) {
size++;
currentNode = currentNode.next;
}
return size;
}
Także tutaj naiwna implementacja polega na każdorazowym zliczaniu wszystkich elementów listy.
Pobieranie elementu z listy
Implementacja tej metody polega na przechodzeniu po wszystkich elementach od początku do żądanego indeksu. Także tutaj implementacja ta nie różni się znacznie od listy jednokierunkowej:
public E get(int index) {
return getNode(index).element;
}
private Node<E> getNode(int index) {
if (isEmpty() || index < 0) {
throw new IndexOutOfBoundsException("Index " + index);
}
Node<E> currentNode = first;
int currentIndex = index;
while (currentIndex > 0) {
if (currentNode == null) {
throw new IndexOutOfBoundsException("Index " + index);
}
currentNode = currentNode.next;
currentIndex--;
}
return currentNode;
}
Dodawanie elementu do listy
W przypadku listy dwukierunkowej węzły zawierają dwa wskaźniki. Operacje modyfikujące taką listę wymagają przepięcia każdego z tych wskaźników. Rysunek poniżej pokazuje przykładowe usunięcie elementu znajdującego się w środku listy:
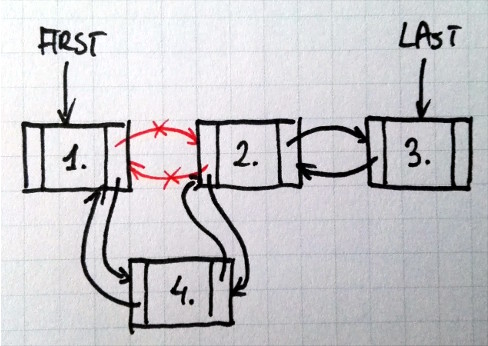
Implementacja tej metody musi obsłużyć dodawanie elementu do pustej listy, dodawanie elementu na koniec i początek listy jak i dodawanie element pomiędzy istniejące węzły:
public boolean add(int index, E element) {
if (first == null && index == 0) {
first = new Node<>(element);
last = first;
return true;
}
Node<E> nodeAtIndex = getNode(index);
// adding at the end of the list
if (nodeAtIndex == null) {
Node<E> previousLast = last;
last = new Node<>(element);
last.previous = previousLast;
previousLast.next = last;
return true;
}
// adding at the beginning of the list
if (nodeAtIndex.previous == null) {
Node<E> previousFirst = first;
first = new Node<>(element);
first.next = previousFirst;
previousFirst.previous = first;
return true;
}
Node<E> newNode = new Node<>(element);
Node<E> previous = nodeAtIndex.previous;
previous.next = newNode;
newNode.previous = previous;
newNode.next = nodeAtIndex;
nodeAtIndex.previous = newNode;
return true;
}
Usuwanie elementu z listy
W tym przypadku także należy zmodyfikować wiele wskaźników. Rysunek poniżej pokazuje jak ta operacja wygląda:
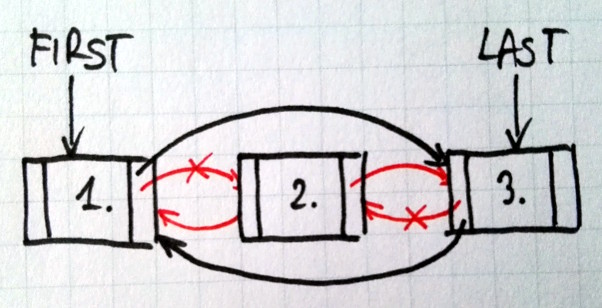
Należy w odpowiedni sposób obsłużyć usuwanie pierwszego i ostatniego elementu. Odpowiednio pierwszy i drugi blok if obsługują te przypadki:
public E remove(int index) {
Node<E> nodeToRemove = getNode(index);
Node<E> previousNode = nodeToRemove.previous;
Node<E> nextNode = nodeToRemove.next;
E removedElement = nodeToRemove.element;
// removing first node
if (previousNode == null) {
if (nextNode == null) {
first = null;
last = null;
}
else {
first = nextNode;
nextNode.previous = null;
}
return removedElement;
}
// removing last node
if (nextNode == null) {
last = previousNode;
previousNode.next = null;
return removedElement;
}
previousNode.next = nextNode;
nextNode.previous = previousNode;
return removedElement;
}
Porównanie złożoności obliczeniowych
Poniższa tabela zawiera zestawienie złożoności obliczeniowych podstawowych operacji dla listy wiązanej i tablicy.
| Operacja | Tablica | Lista wiązana |
|---|---|---|
| pobieranie liczby elementów | Ο(1) |
Ο(1) |
| dodawanie elementu na końcu/początku | Ο(n) |
Ο(1) |
| dodawanie elementu | Ο(n) |
Ο(n) |
| usuwanie elementu na końcu/początku | Ο(n) |
Ο(1) |
| usuwanie elementu | Ο(n) |
Ο(n) |
| pobieranie elementu z końca/początku | Ο(1) |
Ο(1) |
| pobieranie elementu | Ο(1) |
Ο(n) |
Jak widzisz w niektórych przypadkach używając listy wiązanej można uzyskać lepszą złożoność obliczeniową niż w przypadku tablicy.
Najczęściej zadawane pytania
Czym różni się lista wiązana od tablicy
Lista wiązana to struktura, która przetrzymuje elementy rozrzucone w pamięci. Tablica potrzebuje jednolitego obszaru w pamięci komputera. Ponadto tablica ma inne złożoności obliczeniowe niż lista wiązana dla podstawowych operacji pobierania, dodawania czy usuwania elementów.
Kiedy używać listy wiązanej
Na początku mojej przygody z programowaniem mówiono mi, że listy powinno używać się w momencie kiedy nie chcemy zajmować spójnego bloku w pamięci. Nie wydaje mi się, żeby ten argument był nadal bardzo istotny. Dalej jednak ważne są złożoności obliczeniowe zebrane w tabelce wyżej. Jeśli często dodajesz/usuwasz elementy z początku/końca kolekcji i nie potrzebujesz dostępu do innych elementów niż pierwszy/ostatni to lista wiązana jest lepszym wyborem niż tablica.
Czy można odwrócić listę wiązaną
W przypadku listy dwukierunkowej jest to proste. Wystarczy przechodzić po liście od ostatniego elementu do początku. Operacja ta ma złożoność Ο(n). W przypadku listy jednokierunkowej jest to trochę trudniejsze, jednak nadal możliwe do wykonania przy złożoności Ο(n).
Co się dzieje z pominiętymi elementami
W przykładowej implementacji powyżej mogłeś zwrócić uwagę na to, że przepinam wskaźniki na inne elementy. Przez taką manipulację możemy “gubić” instancje klasy Node. Takie instancje nadal zajmują miejsce na stercie. W przypadku Javy z pomocą przychodzi mechanizm “zbierania śmieci” (ang. garbage collection), który wykrywa takie obiekty i usuwa je z pamięci.
Dodatkowe materiały do nauki
Jeśli chcesz spojrzeć na temat z innego punktu widzenia zachęcam Cię do przeczytania materiałów, które zebrałem poniżej:
- Artykuł o liście wiązanej na Wikipedii,
- Artykuł na temat list na Wikibooks,
- Materiały dotyczące list przygotowane przez Jerzego Wałaszka,
- Kod źródłowy przykładów użytych w artykule,
- Implementacja dwukierunkowej listy wiązanej z OpenJDK.
Zadania do wykonania
Skoro już wiesz jak działa lista wiązana nadszedł czas na Twoją implementację. Przygotowałem dla Ciebie dwa zadania do wykonania:
- Zmodyfikuj klasę
SingleLinkedListw taki sposób aby dodawanie elementów na koniec listy miało złożonośćΟ(1). - Dodaj metodę
reverseddo klasSingleLinkedListiDoubleLinkedList. Metoda ta powinna zwrócić nową instancję klasy, w której węzły będą w odwróconej kolejności. - Zmodyfikuj klasy
SingleLinkedListiDoubleLinkedListw taki sposób aby pobieranie rozmiaru listy miało złożonośćΟ(1).
Kod źródłowy klas SingleLinkedList i DoubleLinkedList znajdziesz na samouczkowym githubie.
Na Githubie znajdziesz też testy jednostkowe, pamiętaj o tym żeby sprawdzić czy Twój kod działa poprawnie. Testy powinny Ci w tym pomóc.
Podsumowanie
Po przeczytaniu tego artykułu dokładnie wiesz czym są struktury danych. Poznałeś jednokierunkowe i dwukierunkowe listy wiązane. Zrozumiałeś działanie list na podstawie przykładowej implementacji. Rozwiązując zadania utrwaliłeś swoją wiedzę na temat list. Dobra robota :)!
Jeśli masz jakiekolwiek pytania czy uwagi proszę daj znać w komentarzu, postaram się pomóc. Jeśli nie chcesz pominąć kolejnych artykułów na blogu proszę dopisz się do samouczkowego newslettera i polub Samouczka na Facebooku. Proszę Cię też o podzielenie się linkiem ze znajomymi, może im także przyda się wiedza zgromadzona w tym artykule.
-
Oczywiście zależy to od implementacji listy. W przypadku listy wiązanej otrzymanie takiej złożoności nie jest problemem. ↩
-
Metodę tę można zaimplementować uzyskując złożoność
Ο(1), to będzie Twoim zadaniem na koniec artykułu ;). Uzyskanie takiej złożoności wymaga zmian we wszystkich metodach modyfikujących zawartość listy. ↩
Pobierz opracowania zadań z rozmów kwalifikacyjnych
Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.




Zostaw komentarz