Artykuł ten zawiera jedynie podstawy związane z zagadnieniem złożoności obliczeniowej. Bynajmniej nie wyczerpuje tematu. Teoria obliczeń to osobny dział informatyki. Jeśli chcesz go zgłębić zachęcam Cię do przejrzenia dodatkowych materiałów do nauki.
Mam świadomość, że tłumaczenie złożoności obliczeniowej bez wspominania o maszynie Turinga to profanacja. Jednak dla zupełnie początkujących w temacie takie podejście wydaje mi się łatwiejsze.
Teoria obliczeń
Teoria obliczeń to dział informatyki. Jedną z gałęzi tego działu jest teoria złożoności obliczeniowej. W uproszczeniu można powiedzieć, że zajmuje się ona oszacowaniem wydajności czasowej i pamięciowej algorytmów. Teoria złożoności obliczeniowej bazuje na wielu modelach, które służą do łatwego porównywania algorytmów.
Dlaczego używamy złożoności obliczeniowej
Komputerów na świecie są miliony. Wiele z nich bardzo się od siebie różni. Mają różny procesor, inny moduł RAM. Część z nich używa bardziej wydajnych dysków, które pozwalają na szybszy dostęp do danych. Dla części z nich dane dostępne są na zdalnych maszynach, do których trzeba łączyć się przez sieć. Są też mega-komputery, maszyny o ogromnej mocy obliczeniowej, czy smartfony w kieszeniach.
W związku z tą różnorodnością pojawia się potrzeba wspólnej miary. Miary, która jest niezależna od zmiennych czynników. Może ona pomóc zorientować się w wydajności danego algorytmu, przyporządkować go do zdefiniowanej klasy algorytmów. Tutaj w grę wkraczają modele, o których wspomniałem wcześniej. Modele te upraszczają zawiłości związane z różnorodnością sprzętu.
Mamy zatem wspólną bazę – model. Dalej jednak pozostaje pytanie: w jaki sposób mierzyć wydajność poszczególnych algorytmów? Mierzenie czasu jest mało praktyczne. Na modelu nie możemy mierzyć czasu. Mierzenie czasu nie ma większego sensu na komputerze z powodu różnorodności sprzętu. Otrzymane wyniki nie byłby miarodajne w przypadku innego komputera.
Mierzymy więc zatem liczbę operacji wykonanych na modelu. Następnie próbujemy znaleźć funkcję, która będzie opisywała liczbę operacji w zależności od wejścia algorytmu. Funkcje te możemy porównywać ze sobą.
Przykład wyznaczania złożoności obliczeniowej
Załóżmy że chcemy policzyć sumę elementów tablicy. Może nam w tym pomóc następujący algorytm:
public int sum(int[] numbers) {
int sum = 0;
for (int number : numbers) {
sum += number;
}
return sum;
}
Ile mamy w nim operacji? int sum = 0;, przypisanie to jedna operacja. Następnie mamy pętlę for. Jej ciało zawiera jedną operację. Sama pętla wykona się dokładnie tyle razy ile jest elementów tablicy numbers. Liczbę tych elementów określmy jako n. Na końcu mamy instrukcję return sum;. Jest to ostatnia operacja.
Dodając te operacje do siebie otrzymujemy wzór:
\[f(n) = 1 + n + 1 = n + 2\]Zatem złożoność naszego algorytmu opisana jest przez funkcję f(n) = n + 2.
Tak dla przypomnienia ;). Funkcje możesz pamiętać z matematyki. Na przykład funkcja f(x) = ax^2 + bx + c opisuje parabolę.
Złożoność obliczeniowa a funkcja
Złożoność obliczeniową określamy jako funkcję danych wejściowych algorytmu. Wyznacza się ją jak opisałem w poprzednim punkcie – licząc operacje.
O ile dla naukowców znalezienie dokładnej funkcji może być bardzo istotne, to w praktyce wystarczą jej oszacowania. Takie oszacowania to notacja Ο (dużego O), notacja Ω (omega) i notacja Θ (theta).
Oszacowania rzędu złożoności funkcji
Na tapetę bierzemy przykładową funkcję:
\[f(n) = n^3 - 6n^2 + 4n + 12\]Możemy założyć, że funkcja ta dokładnie opisuje złożoność obliczeniową jakiegoś algorytmu. Argument n to rozmiar danych wejściowych do algorytmu. Wykres1 tej funkcji wygląda następująco:
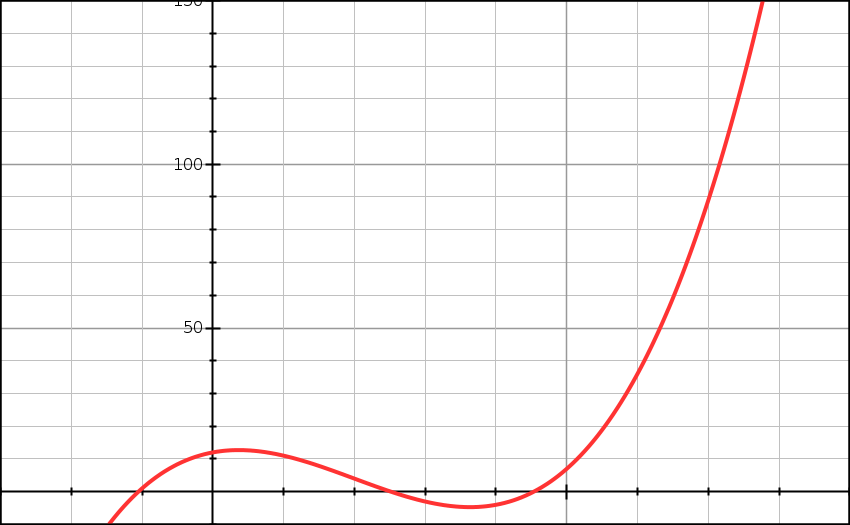
f(n) = n^3 - 6n^2 + 4n + 12
Notacja Ο (dużego O)
Notacja ta zakłada, że istnieje funkcja g(n), dla której spełniona jest poniższa własność:
Teraz przetłumaczę te matematyczne hieroglify :). Własność ta oznacza, że wynik funkcji g(n) pomnożony przez jakąś stałą c będzie większy bądź równy wynikowi funkcji f(n). Własność ta jest spełniona dla wszystkich n, które będą większe od n0. Jeszcze łatwiej wygląda to na wykresie:
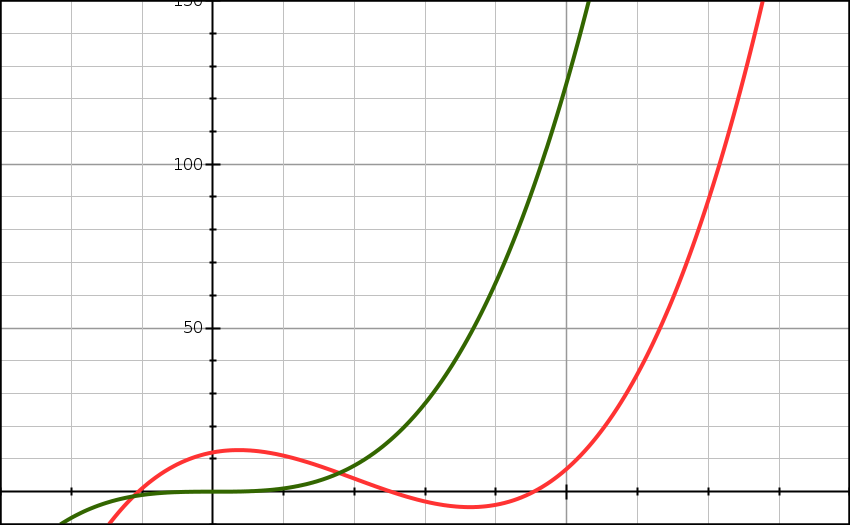
Powyższy wykres pokazuje dwie funkcje. Pierwszą, którą już znasz z poprzedniego wykresu. Druga to wykres funkcji g(n) = n^3. Jak widzisz od pewnego punktu zielona linia jest zawsze ponad czerwoną linią. To nic innego jak oszacowanie z góry. To właśnie jest notacja Ο. Zatem w naszym przypadku nasza funkcja f(n) ma złożoność Ο(n^3).
W mojej dotychczasowej praktyce notacja Ο jest najczęściej spotykana do określania złożoności algorytmów.
Notacja Ο jest oszacowaniem z góry. Zatem można powiedzieć, że jeśli algorytm ma złożoność Ο(n^2) to ma także złożoność Ο(n^3) czy nawet Ο(n!). Jednak Ο(n^2) może być najlepszym oszacowaniem złożoności danego algorytmu.
Z racji tego, że jest to oszacowanie pomijamy w nim wszelkiego rodzaju stałe. Zatem Ο(2n + 123), Ο(2n) i Ο(n) to ta sama złożoność obliczeniowa. Stałe te i tak nie mają znaczenia przy odpowiednio dużych wartościach n.
Pobierz opracowania zadań z rozmów kwalifikacyjnych
Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.
Notacja Ω (omega)
Notacja ta różni się od poprzedniej własnością, którą spełnia nowa funkcja:
\[\forall n \geqslant n_0 : f(n) \geqslant c * g(n)\]Własność ta oznacza, że wynik funkcji g(n) pomnożony przez jakąś stałą c będzie mniejszy bądź równy wynikowi funkcji f(n). Własność ta jest spełniona dla wszystkich n, które będą większe od n0. Ponownie wykres pomoże Ci to zrozumieć:
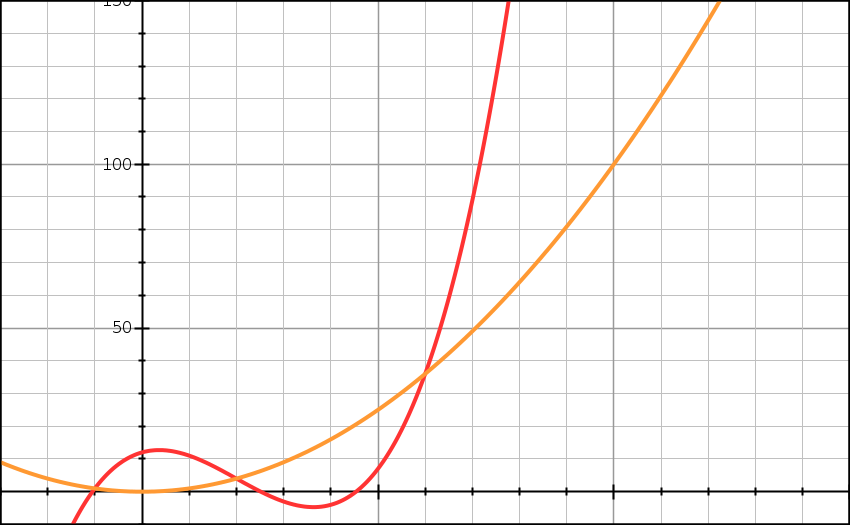
Na wykresie widoczne są dwie funkcje. Pierwszą znasz. Druga to wykres funkcji g(n) = n^2. “Ostatni” punkt przecięcia tych dwóch wykresów, to n02. Od tego miejsca wykres funkcji g(n) jest zawsze pod wykresem funkcji f(n). Możemy powiedzieć, że funkcja f(n) ma złożoność Ω(n^2).
Notacja Θ (theta)
Można powiedzieć, że notacja Θ to połączenie notacji Ο i Ω. W tym przypadku funkcja użyta do oszacowania musi spełniać zależność:
\[\forall n \geqslant n_0 : c_1 * g(n) \geqslant f(n) \geqslant c_2 * g(n)\]Tłumacząc to na polski można powiedzieć, że wynik funkcji g(n) pomnożony przez stałą c1 będzie większy bądź równy wartości funkcji f(n). Jednocześnie będzie mniejszy bądź równy wartości funkcji f(n) jeśli pomnożymy go przez stałą c2. Ponownie wykres może pomóc to zrozumieć:
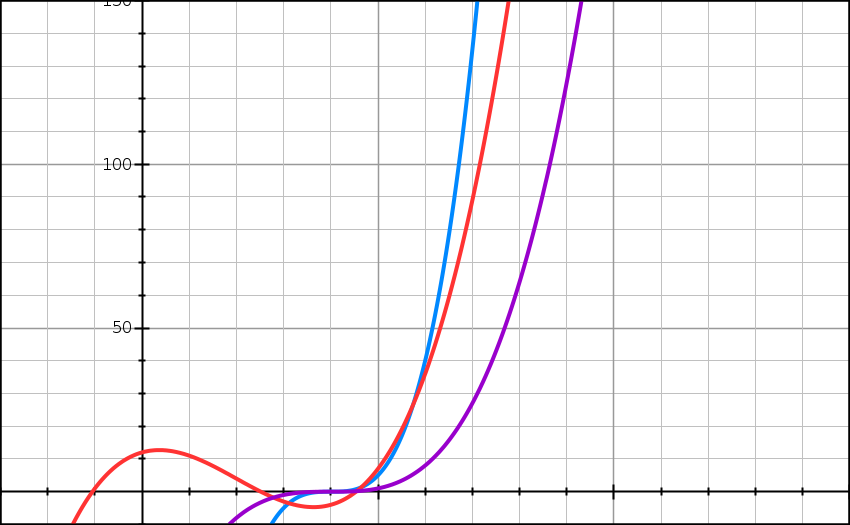
W naszym przypadku funkcję g(n) możemy opisać wzorem g(n) = (n-4)^3. Stałe mają odpowiednio wartości c1 = 5, c2 = 1. Wykres oznaczony kolorem niebieskim to wynik funkcji g(n) przemnożony przez stałą c1. Wykres oznaczony kolorem fioletowym to wynik funkcji g(n) przemnożony przez stałą c2.
Jak wcześniej wspomniałem notacja Ο jest najczęściej spotykana. W dalszej części artykułu będę odnosił się tylko do tej notacji.
Rząd złożoności obliczeniowej
Tu także skupię się na przykładzie wzoru wałkowanego wcześniej:
\[f(n) = n^3 - 6n^2 + 4n + 12\]Jak wspomniałem wcześniej w praktyce nie potrzebujemy tak dokładnego wzoru wystarczy jedynie zgrubne oszacowanie, które uwzględnia najbardziej istotny element funkcji. Który element funkcji jest najbardziej istotny? Ten, który ma największy wpływ na ostateczny wynik funkcji. Jak to sprawdzić? Wystarczy pod n podstawić bardzo dużą liczbę i zobaczyć, który element będzie miał największą wartość. Na przykład:
| Element | Wartość przy n = 1'000'000'000 |
|---|---|
n^3 |
1’000’000’000’000’000’000’000’000’000 |
6n^2 |
6’000’000’000’000’000’000 |
4n |
4’000’000’000 |
12 |
12 |
Jak widzisz, przy odpowiednio dużych wartościach n część “elementów równania” jest mniej istotna. W przypadku funkcji powyżej najszybciej rosnącym elementem jest n^3. Ma on największy wpływ na ostateczny wynik funkcji.
Wiesz już z powyższych rozważań, że funkcja f(n) ma złożoność Ο(n^3). Jest to tak zwana złożoność wielomianowa. Istnieje kilka popularnych rzędów złożoności obliczeniowej.
Ο(1)
Złożoność stała, niezależna od liczby danych wejściowych. Mówimy, że problem o złożoności Ο(1) możemy rozwiązać w stałym czasie niezależnie od wielkości danych wejściowych. Przykład problemu, dla którego istnieje algorytm Ο(1):
Na wejściu programu jest tablica liczb o długości N. Liczby są posortowane rosnąco. Pomiędzy dwoma sąsiadującymi liczbami różnica jest stała. Znajdź sumę liczb w tablicy.
Problem to nic innego jak obliczenie sumy ciągu arytmetycznego. Istnieje na to wzór, który można zaimplementować:
public int sum(int[] numbers) {
if (numbers == null || numbers.length == 0) {
return 0;
}
return (numbers[0] + numbers[numbers.length - 1]) * numbers.length / 2;
}
W tym przypadku nie potrzebujemy iterować po elementach tablicy. Niezależnie od wielkości tablicy wejściowej możemy obliczyć sumę ciągu w stałym czasie.
Ο(n)
Złożoność liniowa. Jest to specyficzny przypadek złożoności wielomianowej. Czas rozwiązania problemu jest wprost proporcjonalny do wielkości danych wejściowych. Przykład problemu, dla którego istnieje algorytm Ο(n):
Na wejściu programu jest tablica liczb o długości N. Znajdź sumę wszystkich liczb w tablicy wejściowej.
public int sum(int[] numbers) {
int sum = 0;
for (int number : numbers) {
sum += number;
}
return sum;
}
Aby znaleźć tę sumę należy sprawdzić wszystkie elementy tablicy. Musimy zatem odbyć N kroków.
Ο(log(n))
Złożoność logarytmiczna, czas rozwiązania zależy od wyniku logarytmu3 z wielkości danych wejściowych. Przykład problemu, dla którego istnieje algorytm Ο(log(n)):
Na wejściu programu jest posortowana tablica liczb o długości N. Sprawdź czy liczba x istnieje w tablicy wejściowej.
To popularny algorytm przeszukiwania binarnego. Jego nazwa pochodzi od tego, że przy każdej iteracji algorytmu dzielimy przeszukiwany zbiór na dwie równe4 części. Algorytmy, które dzielą w ten sposób problem na mniejsze problemy przeważnie są zależne od logarytmu wielkości danych wejściowych.
public boolean binarySearch(int[] numbers, int number) {
int indexLow = 0;
int indexHigh = numbers.length - 1;
while (indexLow <= indexHigh) {
int indexMiddle = indexLow + (indexHigh - indexLow) / 2;
if (number < numbers[indexMiddle]) {
indexHigh = indexMiddle - 1;
}
else if (number > numbers[indexMiddle]) {
indexLow = indexMiddle + 1;
}
else {
return true;
}
}
return false;
}
Ο(nlog(n))
Złożoność liniowo-logarytmiczna. Czas rozwiązania problemu jest wprost proporcjonalny do iloczynu wielkości danych wejściowych i ich logarytmu. Przykładem problemu dla którego istnieje algorytm o złożoności Ο(nlog(n)) jest:
Na wejściu programu jest tablica liczb. Zwróć tablicę, która będzie zawierała te same elementy, które są w tablicy wejściowej. Tablica wynikowa powinna być posortowana w porządku rosnącym.
Powyższy problem to sortowanie. Jeden z ze standardowych problemów w informatyce. Algorytmem sortującym, który ma złożoność obliczeniową Ο(nlog(n)) jest sortowanie przez scalanie (ang. merge sort):
public static int[] sort(int[] numbers) {
if (numbers.length <= 1) {
return numbers;
}
int[] first = new int[numbers.length / 2];
int[] second = new int[numbers.length - first.length];
for (int i = 0; i < first.length; i++) {
first[i] = numbers[i];
}
for (int i = 0; i < second.length; i++) {
second[i] = numbers[first.length + i];
}
return merge(sort(first), sort(second));
}
private static int[] merge(int[] first, int[] second) {
int[] merged = new int[first.length + second.length];
for (int indexFirst = 0, indexSecond = 0, indexMerged = 0; indexMerged < merged.length; indexMerged++) {
if (indexFirst >= first.length) {
merged[indexMerged] = second[indexSecond++];
}
else if (indexSecond >= second.length) {
merged[indexMerged] = first[indexFirst++];
}
else if (first[indexFirst] <= second[indexSecond]) {
merged[indexMerged] = first[indexFirst++];
}
else {
merged[indexMerged] = second[indexSecond++];
}
}
return merged;
}
Algorytm dzieli tablicę na części do czasu aż każda z nich będzie miała długość 1. Następnie scala je ze sobą. Każde takie scalenie to koszt Ο(n). W związku z tym, że tablicę wejściową dzieliliśmy za każdym razem na pół takich scaleń mamy log(n). Zatem wynikowa złożoność algorytmu to Ο(nlog(n)).
Jak widzisz obliczanie złożoności obliczeniowej bardziej skomplikowanych algorytmów nie jest takie łatwe.
Ο(n^2)
Złożoność kwadratowa. Jest to specyficzny przypadek złożoności wielomianowej. Przykładowy problem może być ten, który użyłem wyżej – posortowanie tablicy. Tym razem jednak algorytm jest mniej wydajny. Sortowanie bąbelkowe charakteryzuje się złożonością obliczeniową Ο(n^2):
public int[] sort(int[] numbers) {
for (int i = 0; i < numbers.length; i++) {
for (int j = 0; j < numbers.length - 1; j++) {
if (numbers[j] > numbers[j + 1]) {
int temp = numbers[j + 1];
numbers[j + 1] = numbers[j];
numbers[j] = temp;
}
}
}
return numbers;
}
Mamy tutaj dwie zagnieżdżone pętle. Każda z nich iteruje po n elementach. W związku z tym otrzymujemy złożoność Ο(n^2).
Ο(n^x)
Złożoność wielomianowa. Jak już wiesz złożoność liniowa i złożoność kwadratowa są specyficznymi przypadkami złożoności wielomianowej. Ze względu na częste występowanie wyszczególniłem je jako osobne rzędy złożoności. Przykłady problemów i rozwiązań znajdziesz w poprzednich punktach.
Ο(x^n)
Jest to złożoność wykładnicza, jej przykładem może być Ο(2^n). Problemem, który ma rozwiązanie o złożoności co najmniej Ο(2^n) jest:
Na wejściu programu jest tablica unikalnych liczb. Zwróć tablicę, która będzie zawierała wszystkie możliwe podzbiory elementów tablicy wejściowej.
Wynika to z faktu, że wszystkich możliwych podzbiorów zbioru, który ma n elementów jest dokładnie 2^n. Poniższy algorytm ma złożoność Ο(log(n)2^n).
public static int[][] powerSet(int[] numbers) {
int two_pow_n = 1 << numbers.length;
int[][] powerSet = new int[two_pow_n][];
for (int subsetIndex = 0; subsetIndex < two_pow_n; subsetIndex++) {
powerSet[subsetIndex] = pickNumbers(subsetIndex, numbers);
}
return powerSet;
}
private static int[] pickNumbers(int subsetIndex, int[] numbers) {
int howManyOnes = 0;
int temp = subsetIndex;
while (temp > 0) {
if (temp % 2 == 1) {
howManyOnes++;
}
temp >>= 1;
}
int[] subset = new int[howManyOnes];
for (int charIndex = 0, lastElementIndex = 0; subsetIndex > 0; charIndex++) {
if (subsetIndex % 2 == 1) {
subset[lastElementIndex++] = numbers[charIndex];
}
subsetIndex >>= 1;
}
return subset;
}
Wynika to z faktu, że pętla wewnątrz metody powerSet wywołana jest dokładnie 2^n razy. Natomiast wewnątrz metody pickNumbers są dwie pętle. Każda z nich ma złożoność Ο(log(n)). Zatem finalna złożoność algorytmu to Ο(log(n)2^n).
Spróbuj uruchomić ten kod z tablicą wejściową z 30 elementami, życzę powodzenia ;).
Ο(n!)
Jest to złożoność typu silnia. Dla przypomnienia silnia n, albo inaczej n! to iloczyn wszystkich liczb od 1 do n. Na przykład 3! = 1 * 2 * 3 = 6. Przykładem problemu, dla którego istnieje naiwny algorytm o tej złożoności to problem komiwojażera:
Na wejściu programu jest
nmiast oraz odległości pomiędzy każdą parą miast. Zakładając, że komiwojażer zaczyna z miasta A i ma dojść do miasta B jaką trasę powinien pokonać aby była ona najkrótsza?
Nie silę się nawet na naiwny algorytm dla tego problemu, nie jest on możliwy do uruchomienia na dzisiejszych komputerach dla problemów odpowiednio dużych. Wyobraź sobie, skalę możliwych rozwiązań. (60 - 1)!/2 ~= 6,9 * 10^795. Szacowana liczba atomów wodoru w widzialnym wszechświecie to około 10^80. Przekładając to na problem wyżej, możliwych dróg pomiędzy 60 miastami jest tylko 31% mniej niż atomów wodoru w widzialnym wszechświecie ;).
Najlepszy, średni i najgorszy przypadek
Ten sam algorytm może zachowywać się zupełnie inaczej w przypadku innych danych wejściowych. Nie mówię tu o wielkości problemu, wielkości danych wejściowych. A o instancji problemu.
Jeśli algorytm jako dane wejściowe przyjmuje tablicę liczb to wielkością problemu może być 5 – tablica o długości 5. Natomiast instancji tego problemu jest nieskończenie wiele: [1, 2, 3, 4, 5], [-1, 2, -3, 4, -5] czy [5, 4, 3, 2, 1]. Algorytm może mieć różną złożoność obliczeniową określoną w notacji Ο w zależności od instancji problemu. Są także algorytmy, których złożoność obliczeniowa jest niezależna od instancji problemu.
W zależności od wymagań w wyborze algorytmu bierze się pod uwagę złożoność odpowiedniego przypadku.
Dodatkowe materiały do nauki
Informacji na temat teorii obliczeń i złożoności obliczeniowej w internecie jest sporo. Jednak dość ciężko jest znaleźć jakiekolwiek informacje, które są na początkującym poziomie. Niemniej jednak poniżej starałem się zebrać materiały, które mogą być interesujące:
- Kilka krótkich artykułów opisujących podstawy teorii obliczeń,
- Computational Complexity: A Modern Approach, szkic książki o złożoności obliczeniowej. Jej ostateczna wersja dostępna jest na Amazonie,
- Artykuł na temat złożoności obliczeniowej z uniwersytetu Stanford,
- Sekcja Wolfram Alpha poświęcona złożoności obliczeniowej,
- Artykuł na Wikipedii na temat funkcji służących do szacowania,
- Artykuł o złożoności obliczeniowej na Codility6,
- Fragmenty kodu użyte w tym artykule.
Podsumowanie
Jeśli zrozumiałeś ten artykuł możesz śmiało powiedzieć, że wiesz czym jest złożoność obliczeniowa. Wiesz jak ją szacować, znasz przykłady algorytmów z najczęściej spotykanych rzędów złożoności obliczeniowej. Znasz kilka notacji do określania złożoności. Dowiedziałeś się też ile jest atomów wodoru we wszechświecie ;). W każdym razie masz za sobą spory kawałek lektury i sporo wiedzy.
Na koniec mam do Ciebie prośbę. Proszę podziel się tym artykułem ze swoimi znajomymi, sporo się nad nim napracowałem. Mam nadzieję, że będzie mógł pomóc jak największej grupie osób. Jeśli nie chcesz ominąć kolejnych artykułów w przyszłości polub Samouczka na Facebooku i zapisz się do newslettera. Do następnego razu!
-
Wykresy użyte w tym artykule stworzyłem przy pomocy graphsketch. ↩
-
To oczywiście kolejne uproszczenie, punkt to para dwóch liczb.
n0jest jedną z nich – tą na osi poziomej. Dasz radę wyznaczyć drugą współrzędną? ;) ↩ -
Podstawą logarytmu przeważnie jest 2. Zdarzają się także algorytmy, w których logarytm ma inną podstawę. ↩
-
Oczywiście, w przypadku tablicy o nieparzystej długości jedna z części nie będzie “równiejsza” od drugiej ;). ↩
-
Z pierwszego miasta mamy możliwość pójść do 59 miast, następnie możemy wybrać 58 miast, itd. Wynik dzielony jest przez 2 ponieważ nie ma znaczenia czy pójdziemy z miasta A do miasta B czy odwrotnie. ↩
-
Wielkie dzięki dla Marka za podesłanie linka do tego artykułu. ↩
Pobierz opracowania zadań z rozmów kwalifikacyjnych
Przygotowałem rozwiązania kilku zadań algorytmicznych z rozmów kwalifikacyjnych. Rozkładam je na czynniki pierwsze i pokazuję różne sposoby ich rozwiązania. Dołącz do grupy ponad 6147 Samouków, którzy jako pierwsi dowiadują się o nowych treściach na blogu, a prześlę je na Twój e-mail.




Zostaw komentarz